v = omega * radius For a point \(P\) moving with constant (linear) velocity v along the circumference of a circle of radius \(r\), we have \[v = r\omega\]where \(\omega\) is the . Depresija Latvijā - Depresija. Lai gan depresija ir viena no biežāk sastopamajām psihiskajām saslimšanām, Latvijā ir diezgan nepilnīgs priekšstats par šo slimību, kā arī trūkst izpratnes par to, kad būtu nepieciešama profesionāla palīdzība.
0 · velocity in circular motion v r omega
1 · omega x r rotation
2 · omega vs velocity in circular motion
3 · linear velocity vs omega
4 · how to calculate v omega r
Can left ventricular hypertrophy be cured? LVH can sometimes be reversed when the underlying condition is treated effectively. For others, changes to the left ventricle may be permanent.
All of the above are a "moment of" calculation, with (moment) = →r × (quantity). There is velocity = moment of rotation, torque = moment of force .
1) Radius goes from the axis of rotation to the object (mi personal preference, and the most used in the literature I would say) v = ω ×r v → = ω .In physics, angular velocity (symbol ω or , the lowercase Greek letter omega), also known as angular frequency vector, is a pseudovector representation of how the angular position or orientation of an object changes with time, i.e. how quickly an object rotates (spins or revolves) around an axis of rotation and how fast the axis itself changes direction.Angular velocity is represented by the Greek letter omega (ω, sometimes Ω). It is measured in angle per unit time; hence, the SI unit of angular velocity is radians per second. The dimensional formula of angular velocity is [M 0 L 0 T -1]. For .For a point \(P\) moving with constant (linear) velocity v along the circumference of a circle of radius \(r\), we have \[v = r\omega\]where \(\omega\) is the .
Strategy. In part (a), we are asked to find x, and in (b) we are asked to find ω and v. We are given the number of revolutions θ, the radius of the wheels r, and the angular accelerationn α. .The first relationship in \( v = r \omega, \, or \, \omega = \dfrac{v}{r}\) states that the linear velocity \(v\) is proportional to the distance from the center of rotation, thus, it is largest for a point on the rim (largest \(r\)), as you might expect.

velocity in circular motion v r omega
\[\boldsymbol{v}=\boldsymbol{\omega} \times \boldsymbol{r}\] It is not hard to see that this expression indeed simplifies to the scalar relationship \(v = \omega r\) for . Formula. The Greek symbol omega or ω represents the angular velocity. Mathematically, it is the time rate of change of angular displacement θ. ω = Δθ Δt. Units and Dimensions. The SI unit of angular velocity is radians per .Knowing v and r, we can use the second relationship in v = rω, [latex]\omega=\dfrac{v}{r}[/latex] to calculate the angular velocity. Solution To calculate the angular velocity, we will use the following relationship:
Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site $\begingroup$ You are considering circular motion about a fixed axis. Because the direction of the axis is fixed in space, the concepts "angular velocity is a vector fixed in space, perpendicular to the circular motion" and "angular velocity is the rate of change of your angle $\theta$" amount to the same thing.The angular velocity does not tell us anything about the actual speed of the object, which depends on the radius \(v=\omega R\). This is illustrated in Figure \(\PageIndex{3}\), where two objects can be traveling around two circles of radius \(R_1\) and \(R_2\) with the same angular velocity \(\omega\). If they have the same angular velocity .Now that \(\omega\) is known, the speed \(v\) can most easily be found using the relationship \[v = r\omega,\] where the radius \(r\) ofthe reel is given to be 4.50 cm; thus, \[ v = (0.0450 \, m)(220 \, rad/s) = 9.90 \, m/s.\] Note again that radians must always be used in any calculation relating linear and angular quantities. Also, because .
Now, let us substitute \(v=r \omega\) and \(a= r\alpha\) into the linear equation above: $$ r \omega =r \omega_{0}+ r\alpha t . $$ The radius \(r\) cancels in the equation, yielding $$ \omega =\omega_{0} +a t \left(\text{constant } a\right), $$ . If the plate has a radius of 0.15 m and rotates at 6.0 rpm, calculate the total distance traveled .
Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site Calculate the angular velocity of a 40 cm radius car tire when the car travels at 40 km/h. Solution. Given R = 40 cm = 0.4 m and v = 40 km/h = 40 x 10 3 m/(1 x 3600 s) = 11.11 m/s. Therefore, the angular velocity is. ω = v/R = 11.11 mˑs-1 /0.4 m = 27.8 radˑs-1. Problem 2. How many revolutions does a turntable make if it moves at 36 rad/s and . Tangential velocity V is equal to the angular velocity omega times the radius r: for angular displacement phi, V = omega * r ra > rb Va > Vb When we initially specify the rotation of our object with theta 0, and t0, we should also specify an .Note: With this tool, you can know the radius of a circle anywhere on Google Maps by simply clicking on a single point and extending or moving the circle to change the radius on the Map. Click in the Button Draw a Circle, then Click on map to place the center of the circle and drag at same time to start creating the circle.
A ring of radius R rolls on a horizontal ground with linear speed v and angular speed ω For θ = ± cos − 1 (x v R ω) the velocity of point P is in vertical direction.Find x. ( v < R ω ) . View SolutionTour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site
Omega Centauri (ω Cen, NGC 5139, or Caldwell 80) is a globular cluster in the constellation of Centaurus that was first identified as a non-stellar object by Edmond Halley in 1677. Located at a distance of 17,090 light-years (5,240 parsecs), it is the largest known globular cluster in the Milky Way at a diameter of roughly 150 light-years. [10] It is estimated to contain approximately 10 .Thus the car moves forward at linear velocity \(v = r\omega\), where \(r\) is the tire radius. A larger angular velocity for the tire means a greater velocity for the car. Example \(\PageIndex{1}\): How Fast Does the Car Tire Spin? Calculate .A cicular disc of mass `m` and radius `R` is set into motion on a horizontal floor with a linear speed `v` in the forward direction and an angular speed `omega=(v)/(R)` in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point `O` of the disc.No headers. The cross, or vector, product of two vectors \(\vec A\) and \(\vec B\) is denoted by \(\vec{A} \times \vec{B}\). It is defined as a vector perpendicular to both \(\vec A\) and \(\vec B\) (that is to say, to the plane that contains them both), with a magnitude given by
Relative to the center of mass, point P has velocity −R\(\omega \hat{i}\), where R is the radius of the wheel and \(\omega\) is the wheel’s angular velocity about its axis. Since the wheel is rolling, the velocity of P with respect to the surface is its velocity with respect to the center of mass plus the velocity of the center of mass with .
A sharp corner has a small radius, so that \(a_c\) is greater for tighter turns, as you have probably noticed.It is also useful to express \(a_c\) in terms of angular velocity. Substituting \( v = r\omega \) into the above expression, we find \( a_c = (r \omega^2)/r = r \omega^2 \). We can express the magnitude of centripetal acceleration using .The centripetal force is the force that acts on an object to keep it moving in a circular path. The magnitude of the centripetal force for an object with mass m moving on a circular path (with radius r) at a constant tangential velocity v is given by F c =mv 2 /r the equation where centripetal force is equal to mass times velocity squared, divided by radius of the circular path..
Using cylindrical coordinates $(\rho, \phi, z)$, the angular velocity of the motion is $\boldsymbol\omega = \omega \hat{\mathbf z}$. The velocity is tangent to the circle and given by $\mathbf v = v\hat{\boldsymbol\phi}$. It follows that $$ \boldsymbol\omega \times \mathbf v = \omega v(-\hat{\boldsymbol\rho}) $$
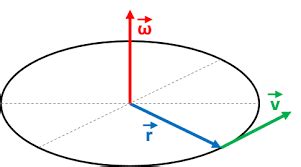
omega x r rotation
I asked her to make sure about this program because I heard somewhere else that LV don't make the sale at the end of each year. they will burn/ destroy the bags instead of put them on sale. How Would LV do trade in the old bags?
v = omega * radius|linear velocity vs omega